Giáo dục > đào tạo > E-learning > ôn thi đại học
Những năm gần đây, Tích phân là một câu không thể thiếu trong mỗi đề thi Đại học và để lấy trọn vẹn 1 điểm câu Tích phân không phải là quá khó. Theo bảng phân tích cấu trúc đề thi đại học môn Toán từ năm 2010 – 2013 thì câu Nguyên hàm, Tích phân có mức độ khó trung bình, thậm chí năm 2013 còn là khá dễ. Tuy nhiên, các bạn cũng không nên chủ quan và mất điểm “vô duyên” khi gặp câu này. Sau đây là bài phân tích và tổng hợp của Hocmai.vn để các bạn có thể lấy trọn vẹn 1 điểm phần Tích phân trong kỳ thi đại học.
1. Nắm vững kiến thức cơ bản về tích phân
Câu Tích phân xuất hiện trong các đề thi đại học thường không quá đánh đố học sinh, học sinh chỉ cần học theo kiến thức ở SGK là có thể làm được. Vì vậy, để có thể làm được câu này, các bạn cần nắm vững được 2 kiến thức cơ bản sau đây:
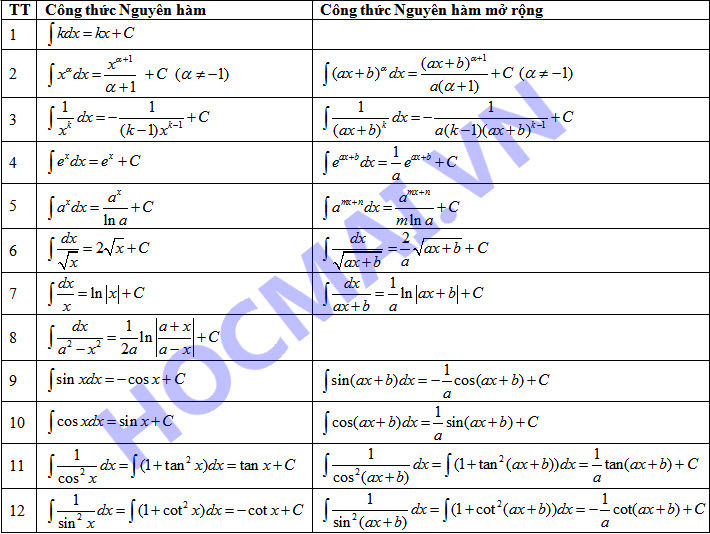
Thứ nhất, các công thức Tích phân cơ bản trong bảng Nguyên hàm
Thứ hai, các phương pháp tính Tích phân, đặc biệt là 2 phương pháp: đổi biến số (thuận, ngược) và Tích phân từng phần.
PHƯƠNG PHÁP ĐỔI BIẾN SỐ

(Trong bài đổi biến số ta nhớ: đặt t = u(x)., (tức đổi biến x sang biến t).
Phải đổi cận x = a t = u(a)
x = b t = u(b)
PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN

Cách đặt: Nhất lốc, nhì đa, tam lượng, tứ mũ (hàm logarit, hàm đa thức, hàm lượng giác, hàm mũ)
2. Một số lỗi cần phải tránh
Sau khi nắm được các kiến thức cơ bản, các bạn cần phải làm đi làm lai thật nhiều bài tập từ dễ đến khó để biết mình còn yếu, hay sai ở những phần nào, bước nào để rút kinh nghiệm. Theo chia sẻ của thầy giáo và nhiều học sinh đang học tập tại Hocmai.vn thì các bạn phải lưu tâm đến 2 vấn đề quan trọng sau:
Vấn đề 1: Sai lầm khi tính Tích phân
- Đổi biến nhưng không đổi cận

- Khi đổi biến không tính vi phân

- Tính Nguyên hàm sai, hiểu sai bản chất công thức

Vấn đề 2: Ứng dụng Tích phân trong hình học
- Tính diện tích hình phẳng:
-
Cách tính dựa vào hình vẽ đã có (tính trực tiếp phần đồ thị cần tính hoặc cách tính gián tiếp)
-
Cách tính không dùng hình vẽ (chú ý để dấu trị tuyệt đối bên trong dấu Tích phân và cách xử lý dấu trị tuyệt đối để tính)
-
Trong một số trường hợp, tính theo biến y sẽ đơn giản hơn tính theo biến x
- Tính thể tích vật thể tròn xoay (chú ý điều kiện áp dụng công thức):
-
Nhận trục Ox làm trục quay:
![chuan]() (chương trình chuẩn)
(chương trình chuẩn) -
Nhận trục Oy làm trục quay:
![nang cao]() (chương trình nâng cao)
(chương trình nâng cao)
3. Mẹo để học và đi thi tốt Tích phân
Ngoài việc nắm vững kiến thức cơ bản và chú ý đến một số lỗi thường gặp ở trên, Hocmai.vn sẽ gợi ý cho các bạn một vài mẹo học và đi thi từ đó dễ dàng định hướng được cách giải bài cũng như kiểm tra lại đáp số để có thể tối đa hóa điểm ở phần Tích phân.
Về cơ bản, Tích phân vốn có nhiều dạng cũng như nhiều phương pháp giải khác nhau nhưng nhìn chung, để giải mỗi bài toán Tích phân thường phải làm theo các bước trong sơ đồ sau. Các bạn có thể tham khảo và lựa chọn hướng tư duy mỗi khi gặp phải bài toán Tích phân.

Bên cạnh đó, vì hiện nay một số máy tính có thể tính được Tích phân nên khi làm bài, ta có thể sử dụng máy tính để tính và sau đấy so lại kết quả xem chính xác hay không. Đồng thời, khi đi thi các bạn cũng nên lưu ý trình bày thật cẩn thận. Đừng quá lạm dụng dấu “=” liên tục trên 1 dòng vì chỉ cần một phép toán sai là coi như cả dòng sai, không được điểm nào. Phải “nhặt điểm” từng tí một: ý 1 được, ý 2 được, ý 3 sai thì cũng được điểm 2 ý đầu. Với mỗi kỳ thi đại học 0,25 điểm cũng là rất quan trọng, quyết định khả năng đỗ trượt của mỗi người vì vậy làm được phần nào phải chắc phần đấy.
Thông tin tham khảo về các khoá luyện thi đại học
| Khoá học | Luyện thi đại học KIT-1 | Chuyên đề Bổ trợ | |
| Nhóm 1 | Nhóm 2 | ||
| Đối tượng tham gia | - Học sinh đã nắm chắc kiến thức căn bản về Tích phân trong chương trình ôn, luyện thi ĐH, CĐ. - Không có nhu cầu học lại những kiến thức căn bản; có nhu cầu tập trung ôn luyện đầy đủ và chuyên sâu kiến thức nằm trong cấu trúc đề thi ĐH, CĐ của Bộ GD&ĐT. | - Học sinh chưa nắm chắc các kiến thức căn bản về Tích phân trong chương trình ôn, luyện thi ĐH, CĐ. - Có nhu cầu học lại kết hợp ôn luyện đầy đủ, chuyên sâu các kiến thức nằm trong cấu trúc đề thi ĐH, CĐ của Bộ GD&ĐT. | - Dành cho học sinh có học lực trung bình trở lên. - có nhu cầu học đầy đủ, kết hợp ôn luyện chuyên sâu các kiến thức về Nguyên hàm. |
| Phương pháp giảng dạy | - Ôn luyện lại phần kiến thức xuất hiện trong cấu trúc đề thi ĐH, CĐ của Bộ GD&ĐT: + Hệ thống hóa lại các kiến thức căn bản. + Hướng dẫn thực hành và củng cố kiến thức thông qua các dạng bài tập mình họa. - Cung cấp phương pháp, kỹ năng, kinh nghiệm trong quá trình làm các dạng bài tập. - Kiểm tra, đánh giá kiến thức theo từng phần kiến thức. | - Ôn luyện lại từng phần kiến thức xuất hiện trong cấu trúc đề thi ĐH, CĐ của Bộ GD&ĐT: + Dạy lại toàn bộ các kiến thức căn bản. + Hướng dẫn thực hành và củng cố kiến thức thông qua các dạng bài tập mình họa. - Cung cấp phương pháp, kỹ năng, kinh nghiệm trong quá trình làm các dạng bài tập. - Kiểm tra, đánh giá kiến thức theo từng phần kiến thức. | - Dạy các kiến thức theo nội dung và cấu trúc chương trình trong SGK. - Cung cấp chi tiết các kiến thức về phương pháp đổi biến số loại 1, loại 2, phương pháp Tích phân từng phần. - Đi sâu vào tính Nguyên hàm và Tích phân của các hàm đặc biệt và hay gặp như: Hàm phân thức hữu tỷ, hàm vô tỷ, hàm lượng giác, hàm siêu việt, hàm có dấu giá trị tuyệt đối. - Ứng dụng kiến thức Nguyên hàm-Tích phân vào tính diện tích hình phẳng và thể tích của khối tròn xoay. - Ôn tập và đánh giá cuối chuyên đề. |




